Studie zur Effizienz und Temperaturrobustheit von gechirpten PPLN-Kristallen im 1064-nm-Frequenzverdopplungsexperiment – ​​02

2. Theoretische Analyse

2.1 Temperaturrobustheit

Unter Temperaturrobustheit versteht man die Stabilität des frequenzverdoppelten Kristalls gegenüber der Temperatur. Insbesondere bei Temperaturschwankungen wird die Leistung des frequenzverdoppelten Lichts nicht wesentlich beeinträchtigt. Der Einfluss der Temperatur auf den Frequenzverdopplungsprozess beruht hauptsächlich auf dem Einfluss auf die Phasenfehlanpassung. Während des Frequenzverdopplungsprozesses kann im Falle einer Kleinsignalnäherung die Leistung des frequenzverdoppelten Lichts wie folgt ausgedrückt werden:

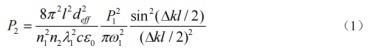
InGleichung 1,list die Länge des Frequenzverdopplungskristalls;D_effist der effektive nichtlineare Koeffizient;Cist die Lichtgeschwindigkeit im Vakuum;ε₀ist die Dielektrizitätskonstante des Vakuums;P_ich,λ_ich,N_ich, Undω_ichSindTDie Leistung, die Wellenlänge, der Brechungsindex und der Strahltaillenradius desFundamentale FrequenzStrahlund Häufigkeit-DoubLEDStrahljeweils. Ter subskriptiertich=1, 2 entsprechen der GrundfrequenzStrahlund die Frequenz verdoppeltStrahljeweils; der Phasenfehlanpassungsbetrag Δk=k₂-2k₁,in welcher Welle vektork_ich=(N_ich2π)/λ_ich. Es kann aus der Gleichung gesehen werden1, dass nur, wenn die Phasenanpassungsbedingung erfüllt ist, das heißt, wenn Δk=0, kann die maximale frequenzverdoppelte optische Leistung erhalten werden. Bei der Quasi-Phasenanpassung wird die Polarisationsperiode künstlich und periodisch geändert, da die spontane Polarisationsrichtung des nichtlinearen Kristalls künstlich und periodisch geändert wirdΛführt den inversen Gittervektor einG_M. Die Beziehung zwischen dem inversen Gittervektor und der Polarisationsperiode ist:

G_M=M(2π/Λ) (2)

WHierMrepräsentiert dieNummerMOrdnung Quasi-Phasenanpassung.DannDie Phasenfehlanpassung im Frequenzverdopplungsprozess kann umgeschrieben werden als:

Δk'=k₂-2k₁-G_M(3)

Es ist aus der bekanntSEllmeier-Gleichung:wWenn sich die Temperatur ändert, ändert sich der BrechungsindexN_ichwird ebenfalls beeinflusst, was sich wiederum auf die Phasenfehlanpassung Δ auswirktk. Seit der Polarisierungsperiode von PPLN(www.wisoptic.com)ist eine einzelne Periode und der eingeführte reziproke Vektor ist ein fester Wert, der mit der Phase Δ übereinstimmtk'= 0 kann nur bei bestimmten Wellenlängen und bestimmten Temperaturbedingungen erreicht werden.daherWir können wissen, dass der Schlüssel zum Erreichen von Temperaturrobustheit darin besteht, die Verstärkungsbandbreite des polarisierten Kristalls zu erweitern, damit der inverse Gittervektor einen bestimmten Bereich abdecken kannUndDie Phasenfehlanpassung kann immer noch Δ erfüllenk'= 0, wenn sich die Temperatur ändert.ICHMit anderen Worten: Die Temperaturrobustheit hängt von der Verstärkungsbandbreite des Kristalls ab. Je größer die Verstärkungsbandbreite, desto besser ist die Temperaturrobustheit des Kristalls. Die Polarisationsperiode von PPLN kann als Funktion der Position ausgedrückt werdenwie folgt:

In der Formel giltD_Gist der Chirp-Grad des CPPLN-Kristalls(www.wisoptic.com), UndΛ₀ist die Anfangsperiode von CPPLN. Es ist zu sehenEGleichung 4, die die Polarisationsperiode von CPPLN abdecktΛ₁= 2πΛ₀UndΛ₂=Λ₀/[(1+D_GΛ₀l)/2π]. Und es ändert sich kontinuierlich innerhalb dieses Bereichs, das heißt, der CPPLN dieser Struktur kann einen inversen Gittervektor bereitstellen, der sich innerhalb eines bestimmten Bereichs kontinuierlich ändert. Wenn sich die Phasenfehlanpassung k innerhalb dieses Bereichs aufgrund der Temperatur ändert, kompensiert der inverse Gittervektor von CPPLN seinen sich ändernden Wert perfekt, um sicherzustellen, dass dies gewährleistet istΔk' = 0Das heißt, die Umwandlungseffizienz von frequenzverdoppeltem Licht kann innerhalb eines bestimmten Temperaturbereichs auf einem sehr hohen Niveau gehalten werden. Es ist jedoch zu beachten, dass es nicht umso besser ist, je größer der Polarisationsperiodenbereich von CPPLN ist, da die Zunahme des Chirps zu einer Verringerung des effektiven nichtlinearen Koeffizienten führt. Daher muss im eigentlichen Produktionsprozess ein Gleichgewicht zwischen Temperaturrobustheit und höchster Frequenzvervielfachungseffizienz hergestellt werden.