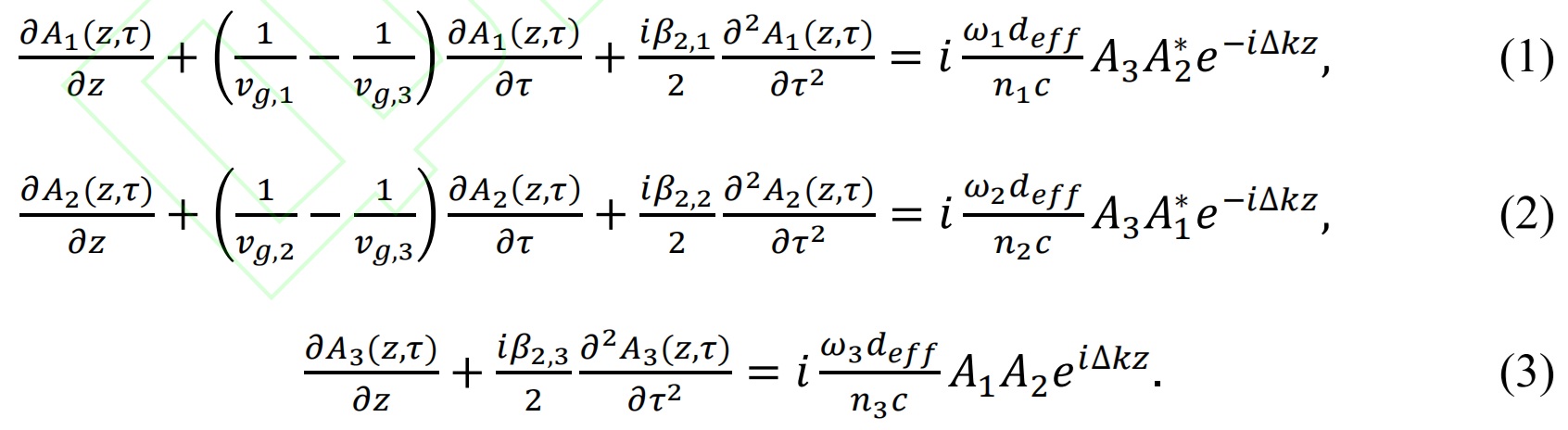Hochleistungs-Ultrakurzpulsquellen im mittleren Infrarotbereich bei 2 - 5 μm basierend auf einer Quelle mit zwei Wellenlängen - Teil 3

2 Theorie und Simulation des mittleren Infrarotbereichs basierend auf der Differenzfrequenzerzeugung von PPLN-Kristallen

Der Prozess der Erzeugung von mittlerem Infrarot durch ultrakurze Impulse im PPLN-Kristall (www.wisoptic.com) wird durch die Drei-Wellen-Kopplungsgleichung beschrieben:

A_ich(Mit,T)stellt die komplexe Amplitude derich-ter Puls,ich = 1, 2 und 3 stellen jeweils das Leerlauf-, Signal- und Pumplicht des Differenzfrequenzprozesses dar.Mit ist die Entfernung entlang der optischen Ausbreitungsrichtung innerhalb des PPLN-Kristalls.T stellt die relative Zeitkoordinate dar, gegeben durchT=T-Mit/v_G,3,Wov_G,ich =Mo_ich/Mk_ichstellt die Gruppengeschwindigkeit derich-ter Puls.B_2,ich ist die Gruppengeschwindigkeitsdispersion derich-ter Puls.Oh_ich UndN₂ stellen die Winkelfrequenz und den Brechungsindex desich-ten Impuls.C ist die Lichtgeschwindigkeit im Vakuum.D_eff ist der effektive nichtlineare Koeffizient, der im PPLN -27,2 pm/V beträgt. Δk =k₃ −k₂ −k₁, stellt die Phasenfehlanpassung dar. Die Beziehung zwischen ∆k und die PPLN-Polarisationsperiode Λ erfüllt |∆k| =2P/L.

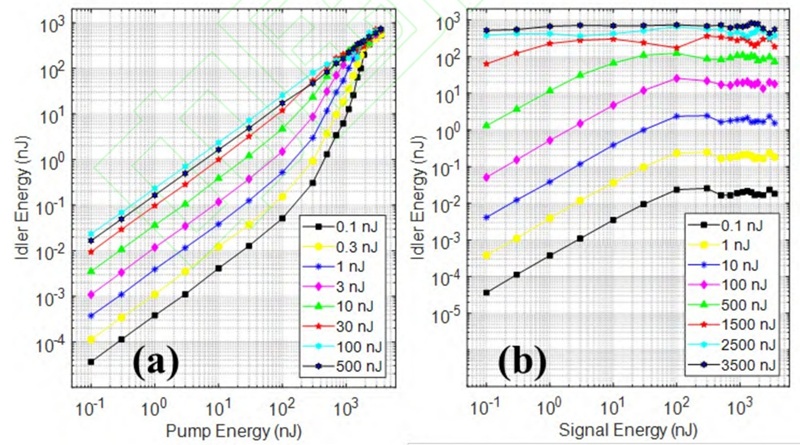
Wenn die Pumpwellenlänge 1,03 μm beträgt, variiert die entsprechende PPLN-Polarisationsperiode zwischen 30,6 μm und 22 μm, während die Ausgangs-Leerlaufwellenlänge zwischen 2,1 μm und 6 μm variiert (Signalwellenlänge 1,24 μm bis 2,02 μm). Um die nichtlineare Wechselwirkung zwischen Pump- und Signallicht im PPLN-Kristall zu untersuchen, haben wir die Gleichungen 1-3 mit der Split-Step-Fourier-Methode gelöst. Abbildung 2 stellt die Ausgangs-Leerlaufenergie gegenüber der Pumpenergie dar, während die Signalenergie zwischen 0,1 nJ und 500 nJ variiert (Abbildung 2(a)), und die Ausgangs-Leerlaufenergie gegenüber der Signalenergie, während die Pumpenergie zwischen 0,1 nJ und 3,5 μJ variiert (Abbildung 2(b)). Die zentralen Wellenlängen des Pump- und Signallichts betrugen 1,03 μm bzw. 1,55 μm bei einer Pulsbreite von 300 fs. Die Pulsenergie variierte zwischen 0,1 nJ und 3,5 μJ. Der PPLN-Kristall war 3 mm dick und hatte eine Polarisationsperiode von 29,7 μm. Der Punktdurchmesser in der Kristallmitte betrug 150 μm. Die anfängliche Verzögerung wurde auf 165 fs eingestellt, um sicherzustellen, dass die Spitzen der Pump- und Signallichtimpulse in der Kristallmitte zusammenfielen.

Abb. 2. Die Simulationskurve der Leerlauflichtenergie variiert mit der Pumplicht- und Signallichtenergie. 

Wie in Abbildung 2 (a) gezeigt, funktioniert der DFG -Prozess im linearen Bereich, wenn die Pumpenleistung niedrig ist (<100 NJ). Bei allen Signalimpulsergien nimmt die Idler -Leistung mit zunehmender Pumpenleistung linear zu. Mit zunehmender Pumpenleistung (100NJ-2000NJ) tritt der DFG-Prozess in die exponentielle Region ein, in der die Idler-Leistung exponentiell mit der Pumpenleistung zunimmt. Der exponentielle Anstieg wird durch eine abnehmende Signalleistung stärker ausgeprägt. Wenn die Signalimpulsenergie 100NJ beträgt, zeigt die Idler -Leistung sogar einen abnehmenden Trend, da die Pumpenleistung von 700 NJ bis 1000 NJ variiert. Wenn die Pumpenleistung 2000NJ überschreitet, arbeitet der DFG -Prozess im Sättigungsbereich. Die Idler -Leistung nimmt mit zunehmender Pumpenleistung langsamer zu, und die Signalleistung hat nur geringe Auswirkungen auf die Ausgangs -Idlerleistung. Wenn jedoch die Signallichtergie von 0,1NJ auf 500 NJ zunimmt, nimmt der Pumpenpuls -Energieschwellenwert für DFG in den Sättigungsbereich von 2000NJ auf 700 NJ ab. Die Ergebnisse in Abbildung 2 (b) zeigen, dass die Kurve der Ausgangs -Idler -Licht -Energie und Signallichtenergie einen linearen Bereich und einen Sättigungsbereich umfasst. Im linearen Bereich sind die Pumpen- und Signallichtenergien niedrig und die Wechselwirkung schwach. Mit zunehmender Signallichtergie erreicht die Ausgangs -Idler -Licht -Energie eine Sättigung und die Schwingung tritt auf. Zunehmende Signallichtenergie kann zu einer Abnahme der Ausgangs -Idler -Lichtergie führen, was mit den Ergebnissen übereinstimmt, die durch hellblaue und schwarze hexagonale Sterne in Abbildung 2 (a) gezeigt werden. Ähnlich wie in Abbildung 2 (a), wenn die Pumpenlichtenergie von 0,1 NJ auf 3,5 μJ zunimmt, nimmt die für DFG erforderliche Signallichtergie für den Eintritt in den Sättigungsbereich von 100 NJ auf 0,1 NJ ab.